TẬP HỢP
I – LÝ THUYẾT:
1. Tập hợp: (còn gọi là tập) là một khái niệm cơ bản của Toán học, không định nghĩa.
– Thường kí hiệu: ![]() ,
, ![]() , …
, …
*. Để chỉ ![]() là một phần tử của tập hợp
là một phần tử của tập hợp ![]() ta viết
ta viết ![]() (đọc là
(đọc là ![]() thuộc
thuộc ![]() ).
).
**. Để chỉ ![]() không phải là một phần tử của tập hợp
không phải là một phần tử của tập hợp ![]() ta viết
ta viết ![]() (đọc là
(đọc là ![]() không thuộc
không thuộc ![]() ).
).
– Hai cách thường dùng để xác định một tập hợp:
*. Liệt kê các phần tử của tập hợp.
**. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Chú ý: Người ta thường minh họa tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven.
2. Tập hợp rỗng: là tập hợp không chứa phần tử nào. Kí hiệu: ![]()
3. Tập hợp con: Nếu mọi phần tử của tập ![]() đều là phần tử của tập
đều là phần tử của tập ![]() thì ta nói
thì ta nói ![]() là một tập hợp con của B, viết là
là một tập hợp con của B, viết là ![]() ( đọc là
( đọc là ![]() chứa trong
chứa trong ![]() ).
).
![]()
Tính chất:
|
|
|
|
4. Tập hợp bằng nhau: ![]() và
và ![]() thì ta nói tập hợp
thì ta nói tập hợp ![]() bằng tập hợp
bằng tập hợp ![]() , viết là:
, viết là: ![]() .
.
![]()
CÁC DẠNG TOÁN
Chủ đề 1. PHẦN TỬ – TẬP HỢP
A – VÍ DỤ:
Vd1: Kí hiệu nào sau đây dùng để viết đúng mệnh đề “ ![]() là số tự nhiên”?
là số tự nhiên”?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Lời giải
Chọn B: ![]()
Vd2: Kí hiệu nào sau đây dùng để viết đúng mệnh đề “ ![]() không phải là số hữu tỉ ”
không phải là số hữu tỉ ”
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Lời giải
Chọn C: ![]()
Vd3: Liệt kê các phần tử của các tập hợp:
a/. Tập ![]() các số tự nhiên chia hết cho 3 và nhỏ hơn 25:
các số tự nhiên chia hết cho 3 và nhỏ hơn 25:
b/. ![]()
c/. ![]()
d/. ![]()
Lời giải
a/. Cách 1: ![]() = {0; 3; 6; 9; 12; 15; 18; 21; 24}.
= {0; 3; 6; 9; 12; 15; 18; 21; 24}.
Cách 2: Là bội của 3 và nhỏ hơn 25.
b/. Cách 1: ![]() = {0; 1; 2; 3}
= {0; 1; 2; 3}
Cách 2: Bấm máy tính
c/. ![]() = { – 1; 3}: Giải phương trình tích.
= { – 1; 3}: Giải phương trình tích.
d/. ![]() = {–3; –1; 1; 3; 5}:
= {–3; –1; 1; 3; 5}:
Cách giải: Bấm máy tính biểu thức 2k+1. Nhập các giá trị của k ![]()
B – BÀI TẬP TỰ LUYỆN:
Câu 1. Cho ![]() là một tập hợp. Trong các mệnh đề sau, mệnh đề nào đúng
là một tập hợp. Trong các mệnh đề sau, mệnh đề nào đúng
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 2. Cho ![]() là một phần tử của tập hợp
là một phần tử của tập hợp ![]() Xét các mệnh đề sau:
Xét các mệnh đề sau:
(I) ![]() (II)
(II) ![]() (III)
(III) ![]() (IV)
(IV) ![]()
Trong các mệnh đề trên, mệnh đề nào đúng?
A. I và II. B. I và III. C. I và IV. D. II và IV.
Câu 3. Mệnh đề nào sau đây tương đương với mệnh đề ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Đáp án: 1C, 2C, 3B.
Chủ đề 2. XÁC ĐỊNH TẬP HỢP
A – VÍ DỤ:
Vd1: Hãy liệt kê các phần tử của tập ![]()
A. ![]() B.
B. ![]() C.
C. 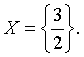 D.
D. 
Lời giải
Chọn D: 
Cách giải: Giải pt bậc hai 2x2 – 5x + 3 = 0 ó x = 1; x = 3/2.
Vd2: Tìm một tính chất đặc trưng cho các phần tử của mỗi tập hợp sau:
a/. ![]() b/.
b/. 
Lời giải
a/. ![]() b/.
b/. 
B – BÀI TẬP TỰ LUYỆN:
Câu 1. Cho tập ![]() Tính tổng
Tính tổng ![]() các phần tử của tập
các phần tử của tập ![]()
A. ![]() B.
B.  C.
C. ![]() D.
D. ![]()
Câu 2. Cho tập  Hỏi tập
Hỏi tập ![]() có bao nhiêu phần tử?
có bao nhiêu phần tử?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 3. Hãy liệt kê các phần tử của tập ![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Câu 4. Hãy liệt kê các phần tử của tập ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 5. Cho tập hợp ![]() là ước chung của
là ước chung của ![]() . Hãy liệt kê các phần tử của tập hợp
. Hãy liệt kê các phần tử của tập hợp ![]() .
.
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Câu 6. Hỏi tập hợp ![]() có bao nhiêu phần tử?
có bao nhiêu phần tử?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 7. Tập hợp nào sau đây là tập rỗng?
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Câu 8. Cho tập ![]() và
và ![]() Hỏi tập
Hỏi tập ![]() có bao nhiêu phần tử ?
có bao nhiêu phần tử ?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Đáp án: 1D, 2C, 3C, 4C, 5A, 6C, 7B, 8C.
Chủ đề 3. TẬP CON
A – VÍ DỤ:
Vd1: Cho ![]() = {1; 3; 5}. Liệt kê các tập con của tập
= {1; 3; 5}. Liệt kê các tập con của tập ![]()
Lời giải
Các tập con của ![]() bao gồm: {1}, {3}, {5}, {1; 3}, {1; 5}, {3; 5}, {1; 3; 5},
bao gồm: {1}, {3}, {5}, {1; 3}, {1; 5}, {3; 5}, {1; 3; 5}, ![]()
Vd2: Hình nào sau đây minh họa tập ![]() là con của tập
là con của tập ![]() ?
?
A. 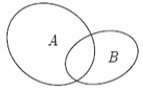 B.
B. 
C.  D.
D. 
Lời giải
Chọn C.
Vd3: Cho tập ![]() Hỏi tập
Hỏi tập ![]() có bao nhiêu tập hợp con?
có bao nhiêu tập hợp con?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Lời giải
Chọn A. Số tập con: 24 = 16. (Số tập con của tập có n phần tử là 2n )
B – BÀI TẬP TỰ LUYỆN:
Câu 1. Cho tập ![]() Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
A. Số tập con của ![]() là
là ![]() B. Số tập con của
B. Số tập con của ![]() có hai phần tử là
có hai phần tử là ![]()
C. Số tập con của ![]() chứa số 1 là
chứa số 1 là ![]() D. Số tập con của
D. Số tập con của ![]() chứa 3 phần tử là
chứa 3 phần tử là ![]()
Câu 2. Tập ![]() có bao nhiêu tập hợp con có đúng hai phần tử?
có bao nhiêu tập hợp con có đúng hai phần tử?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 3. Trong các tập hợp sau, tập nào có đúng một tập hợp con ?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 4. Trong các tập hợp sau, tập nào có đúng hai tập hợp con ?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 5. Cho hai tập hợp ![]() và
và ![]() Có tất cả bao nhiêu tập
Có tất cả bao nhiêu tập ![]() thỏa
thỏa ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 6. Cho hai tập hợp ![]() và
và ![]() Có tất cả bao nhiêu tập
Có tất cả bao nhiêu tập ![]() thỏa
thỏa ![]() và
và ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 7. Cho các tập hợp sau:
![]() là bội số của
là bội số của ![]() .
. ![]() là bội số của
là bội số của ![]() .
.
![]() là ước số của
là ước số của ![]() .
. ![]() là ước số của
là ước số của ![]() .
.
Mệnh đề nào sau đây đúng?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Đáp án: 1B, 2B, 3A, 4B, 5A, 6D, 7B.