MỘT SỐ KĨ NĂNG GIẢI HỆ PHƯƠNG TRÌNH

Trong các đề thi đại học những năm gần đây , ta gặp rất nhiều bài toán về hệ phương trình . Nhằm giúp các bạn ôn thi tốt , bài viết này tôi xin giới thiệu một số dạng bài và kĩ năng giải chúng

I.HỆ SỬ DỤNG PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG.

Đặc điểm chung của dạng hệ này là sử dụng các kĩ năng biến đổi đồng nhất đặc biệt là kĩ năng phân tích nhằm đưa một PT trong hệ về dạng đơn giản ( có thể rút theo y hoặc ngược lại ) rồi thế vào PT còn lại trong hệ .

*Loại thứ nhất , trong hệ có một phương trình bậc nhất với ẩn x hoặc y khi đó ta tìm cách rút y theo x hoặc ngược lại

Ví dụ 1 . Giải hệ phương trình

Giải.

Dễ thấy x = 0 không thỏa mãn PT(2) nên từ (2) ta có : thay vào (1) ta được

Từ đó , ta được các nghiệm của hệ là : (1;-1) , (-2; )

*Loại thứ hai , Một phương trình trong hệ có thể đưa về dạng tích của các phương trình bậc nhất hai ẩn

Ví dụ 2 . Giải hệ phương trình

Giải .

Điều kiện : x≥1 ; y≥0

PT (1) ( từ điều kiện ta có x+y>0)

thay vào PT (2) ta được :

*loại thứ ba , đưa một phương trình trong hệ về dạng phương trình bậc hai của một ẩn , ẩn còn lại là tham số

Ví dụ 3. Giải hệ phương trình

Giải .

Biến đổi PT (2) về dạng

Coi PT (2) là phương trình ẩn y tham số x ta có từ đó ta được nghiệm

Thay (3) vào (1) ta được :

Thay (4) vào (1) ta được :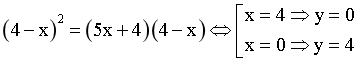

Vậy nghiệm của hệ là : (0;4) , (4;0) , ( ;0)

II.HỆ SỬ DỤNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ

Điểm quan trọng nhất trong hệ dạng này là phát hiện ẩn phụ có ngay trong từng phương trình hoặc xuất hiện sau một phép biến đổi hằng đẳng thức cơ bản hoặc phép chia cho một biểu thức khác 0.

Ví dụ 4. Giải hệ phương trình

Giải .

Dễ thấy y=0 không thỏa mãn PT(1) nên HPT

Đặt 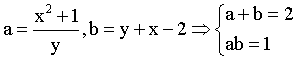giải hệ ta được a=b=1 từ đó ta có hệ

Hệ này bạn đọc có thể giải dễ dàng.

Ví dụ 5. Giải hệ phương trình

Giải . Điều kiện : x +y ≠0

HPT

Đặt 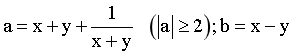ta được hệ

Giải hệ ta được a=2 , b=1 ( do |a|≥2 ) từ đó ta có hệ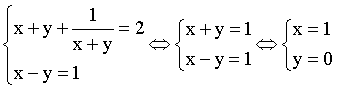

III.HỆ SỬ DỤNG PHƯƠNG PHÁP HÀM SỐ

Hệ loại này ta gặp nhiều ở hai dạng f(x)=0 (1)và f(x)=f(y) (2) với f là hàm đơn điệu trên tập D và x,y thuộc D .Nhiều khi ta cần phải đánh giá ẩn x,y để x,y thuộc tập mà hàm f đơn điệu

* Loại thứ nhất , một phương trình trong hệ có dạng f(x)=f(y) , phương trình còn lại giúp ta giới hạn x,y thuộc tập D để trên để trên đó hàm f đơn điệu

Ví dụ 6 . Giải hệ phương trình

Giải .

Từ PT (2) ta có

Xét hàm số có do đó f(t) nghịch biến trên

khoảng (-1;1) hay PT (1) thay vào PT (2) ta được PT :

Đặt a=x⁴ ≥0 và giải phương trình ta được

*loại thứ hai , là dạng hệ đối xứng loại hai mà khi giải thường dẫn đến cả hai trường hợp (1) và (2)

Ví dụ 7. Giải hệ phương trình

Giải .

Đặt ta được hệ

Trừ vế với vế 2 PT ta được : (3)

Xét hàm số

Vì do đó hàm số f(t) đồng biến trên R

Nên PT (3) thay vào PT (1) ta được (4)

Theo nhận xét trên thì nên PT (4) ( lấy ln hai vế )

Xét hàm số

hay hàm g(a) nghịch biến trên R và do PT (4) có nghiệm a=0 nên PT (4) có nghiệm duy nhất a=0

Từ đó ta được nghiệm của hệ ban đầu là : x=y=1

IV.HỆ SỬ DỤNG PHƯƠNG PHÁP ĐÁNH GIÁ

Với phương pháp này, cần lưu ý phát hiện các biểu thức không âm và nắm vững cách vận dụng các bất đẳng thức cơ bản

Ví dụ 8 . Giải hệ phương trình

Giải.

Cộng vế với vế hai PT ta được (1)

Ta có :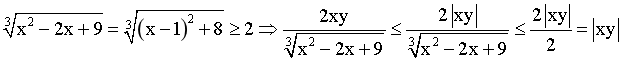

Tương tự mà theo bất đẳng thức Côsi nên VT(1)≤VP(1)

Dấu bằng xảy ra khi thử lại ta được nghiệm của hệ là : (0;0) , (1;1)

Ví dụ 9 . Giải hệ phương trình

Giải.

HPT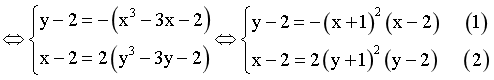

Nếu x>2 từ (1) suy ra y-2<0 diều này mâu thuẫn với PT(2) có (x-2) và (y-2) cùng dấu

Tương tự với x<2 ta cũng suy ra điều vô lí . Vậy nghiệm của hệ là x=y=2

Hy vọng một số ví dụ trên sẽ giúp bạn phần nào kĩ năng giải hệ .Để kết thúc bài viết mời các bạn cùng giải các hệ phương trình sau