HỆ TRỤC TỌA ĐỘ
I – LÝ THUYẾT
1. Trục và độ dài đại số trên trục
a)Định nghĩa
- Trục tọa độ (hay gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm
 gọi là điểm gốc và một vectơ đơn vị
gọi là điểm gốc và một vectơ đơn vị 
- Điểm
 gọi là gốc tọa độ.
gọi là gốc tọa độ. - Hướng của vecto đơn vị là hướng của trục.
- Ta kí hiệu trục đó là



b) Cho ![]() là một điểm tùy ý trên trục
là một điểm tùy ý trên trục ![]() Khi đó có duy nhất một số
Khi đó có duy nhất một số ![]() sao cho k
sao cho k ![]() Ta gọi số
Ta gọi số ![]() đó là tọa độ của điểm
đó là tọa độ của điểm ![]() đối với trục đã cho.
đối với trục đã cho.
c) Cho hai điểm ![]() và
và ![]() trên trục
trên trục ![]() Khi đó có duy nhất số
Khi đó có duy nhất số ![]() sao cho a
sao cho a ![]() Ta gọi số
Ta gọi số ![]() là độ dài đại số của vectơ
là độ dài đại số của vectơ ![]() đối với trục đã cho và kí hiệu
đối với trục đã cho và kí hiệu ![]()
Nhận xét.
![]() Nếu
Nếu ![]() cùng hướng với
cùng hướng với ![]() thì
thì ![]() còn nếu
còn nếu ![]() ngược hướng với
ngược hướng với ![]() thì
thì ![]()
![]() Nếu hai điểm
Nếu hai điểm ![]() và
và ![]() trên trục
trên trục ![]() có tọa độ lần lượt là
có tọa độ lần lượt là ![]() và
và ![]() thì
thì ![]()
2. Hệ trục tọa độ
a) Định nghĩa. Hệ trục tọa độ ![]() gồm hai trục
gồm hai trục ![]() và
và ![]() vuông góc với nhau. Điểm gốc
vuông góc với nhau. Điểm gốc ![]() chung của hai trục gọi là gốc tọa độ. Trục
chung của hai trục gọi là gốc tọa độ. Trục ![]() được gọi là trục hoành và kí hiệu là
được gọi là trục hoành và kí hiệu là ![]() trục
trục ![]() được gọi là trục tung và kí hiệu là
được gọi là trục tung và kí hiệu là ![]() Các vectơ
Các vectơ ![]() và
và ![]() là các vectơ đơn vị trên
là các vectơ đơn vị trên ![]() và
và ![]() và
và ![]() Hệ trục tọa độ
Hệ trục tọa độ ![]() còn được kí hiệu là
còn được kí hiệu là ![]()

Mặt phẳng mà trên đó đã cho một hệ trục tọa độ ![]() còn được gọi là mặt phẳng tọa độ
còn được gọi là mặt phẳng tọa độ ![]() hay gọi tắt là mặt phẳng
hay gọi tắt là mặt phẳng ![]()
b) Tọa độ của vectơ
Trong mặt phẳng ![]() cho một vectơ
cho một vectơ ![]() tùy ý. Vẽ
tùy ý. Vẽ ![]() và gọi
và gọi ![]() lần lượt là hình chiếu của vuông góc của
lần lượt là hình chiếu của vuông góc của ![]() lên
lên ![]() và
và ![]() Ta có
Ta có ![]() và cặp số duy nhất
và cặp số duy nhất ![]() để
để ![]() Như vậy
Như vậy ![]()
Cặp số ![]() duy nhất đó được gọi là tọa độ của vectơ
duy nhất đó được gọi là tọa độ của vectơ ![]() đối với hệ tọa độ
đối với hệ tọa độ ![]() và viết
và viết ![]() hoặc
hoặc ![]() Số thứ nhất
Số thứ nhất ![]() gọi là hoành độ, số thứ hai
gọi là hoành độ, số thứ hai ![]() gọi là tung độ của ve ctơ
gọi là tung độ của ve ctơ ![]()

Như vậy
![]()
Nhận xét. Từ định nghĩa tọa độ của vectơ, ta thấy hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
Nếu ![]() và
và ![]() thì
thì 
Như vậy, mỗi vectơ được hoàn toàn xác định khi biết tọa độ của nó.
c) Tọa độ của một điểm
Trong mặt phẳng tọa độ ![]() cho một điểm
cho một điểm ![]() tùy ý. Tọa độ của vectơ
tùy ý. Tọa độ của vectơ ![]() đối với hệ trục
đối với hệ trục ![]() được gọi là tọa độ của điểm
được gọi là tọa độ của điểm ![]() đối với hệ trục đó.
đối với hệ trục đó.
Như vậy, cặp số ![]() là tọa độ của điểm
là tọa độ của điểm ![]() khi và chỉ khi
khi và chỉ khi ![]() Khi đó ta viết
Khi đó ta viết ![]() hoặc
hoặc ![]() Số
Số ![]() được gọi là hoành độ, còn số
được gọi là hoành độ, còn số ![]() được gọi là tung độ của điểm
được gọi là tung độ của điểm ![]() Hoành độ của điểm
Hoành độ của điểm ![]() còn được kí hiệu là
còn được kí hiệu là ![]() tung độ của điểm
tung độ của điểm ![]() còn được kí hiệu là
còn được kí hiệu là ![]()
![]()


Chú ý rằng, nếu ![]() thì
thì ![]()
d) Liên hệ giữa tọa độ của điểm và tọa độ của vectơ trong mặt phẳng
Cho hai điểm ![]() và
và ![]() Ta có
Ta có
![]()
3. Tọa độ của các vectơ ![]()
Ta có các công thức sau:
| Cho Khi đó:
|
Nhận xét. Hai vectơ ![]() với
với ![]() cùng phương khi và chỉ khi có một số
cùng phương khi và chỉ khi có một số ![]() sao cho
sao cho ![]() và
và ![]()
4. Tọa độ trung điểm của đoạn thẳng. Tọa độ trọng tâm của tam giác
a) Cho đoạn thẳng ![]() có
có ![]() Ta dễ dàng chứng minh được tọa độ trung điểm
Ta dễ dàng chứng minh được tọa độ trung điểm ![]() của đoạn thẳng
của đoạn thẳng ![]() là
là

b) Cho tam giác ![]() có
có ![]() Khi đó tọa độ của trọng tâm
Khi đó tọa độ của trọng tâm ![]() của tam giác
của tam giác ![]() được tính theo công thức
được tính theo công thức
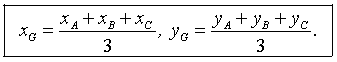
II – DẠNG TOÁN
- 1. Dạng 1: Tìm tọa độ của một điểm; tọa độ vectơ; độ dài đại số của vectơ và chứng minh hệ thức liên quan trên trục
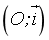
- Phương pháp giải.
Sử dụng các kiến thức cơ bản sau:
- Trên trục
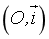 , điểm
, điểm  có tọa độ
có tọa độ 
- Trên trục
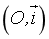 , vecto
, vecto  có tọa độ
có tọa độ 
- Vectơ
 có độ dài đại số là
có độ dài đại số là 
- Nếu
 lần lượt là tọa độ của
lần lượt là tọa độ của  thì
thì 
- Tọa độ trung điểm
 của đoạn
của đoạn  là:
là: 
- Các tính chất:
+ ![]()
+ ![]()
+ ![]()
A. VÍ DỤ MINH HỌA
Ví dụ 1: Trên trục tọa độ ![]() cho 2 điểm
cho 2 điểm ![]() có tọa độ lần lượt là
có tọa độ lần lượt là ![]() Tọa độ của vecto
Tọa độ của vecto ![]() là:
là:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Lời giải
Chọn B.
Ta có: ![]()
Ví dụ 2: Trên trục tọa độ ![]() cho 2 điểm
cho 2 điểm ![]() có tọa độ lần lượt
có tọa độ lần lượt ![]() và
và ![]() . Tọa độ trung điểm
. Tọa độ trung điểm ![]() của
của ![]() là :
là :
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Lời giải
Chọn D.
Tọa độ điểm ![]() là:
là: 
Ví dụ 3: Trên trục ![]() cho 3 điểm
cho 3 điểm ![]() có tọa độ lần lượt là
có tọa độ lần lượt là ![]() . Tìm điểm
. Tìm điểm ![]() sao cho
sao cho ![]()
A.  B.
B. 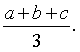 C.
C. 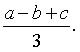 D.
D. 
Lời giải
Chọn D.
Gọi điểm ![]() có tọa độ là
có tọa độ là ![]() .
.


Ví dụ 4: Trên trục ![]() , cho ba điểm
, cho ba điểm ![]() lần lượt có tọa độ là
lần lượt có tọa độ là ![]() . Tìm tọa độ điểm
. Tìm tọa độ điểm ![]() thỏa mãn
thỏa mãn ![]() .
.
A. ![]() . B.
. B. ![]() . C.
. C. ![]() D.
D. ![]() .
.
Lời giải
Chọn C.
Gọi điểm ![]() có tọa độ là
có tọa độ là ![]() .
.

![]()
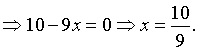
B. BÀI TẬP TỰ LUYỆN
- Trên trục
 , cho ba điểm
, cho ba điểm  lần lượt có tọa độ là
lần lượt có tọa độ là  . Tìm tọa độ điểm
. Tìm tọa độ điểm  sao cho
sao cho  .
.
A. ![]() . B.
. B. ![]() C.
C. ![]() D.
D. ![]()
- Trên trục
 , cho ba điểm
, cho ba điểm  lần lượt có tọa độ là
lần lượt có tọa độ là  . Độ dài đại số của
. Độ dài đại số của 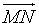 là:
là:
A. ![]() . B.
. B. ![]() C.
C. ![]() D.
D. ![]()
- 2. DẠNG 2: Tìm tọa độ điểm, tọa độ vectơ trên mặt phẳng
 .
. - Phương pháp giải.
- Để tìm tọa độ của vectơ
 ta làm như sau
ta làm như sau
Dựng vectơ ![]() . Gọi
. Gọi ![]() lần lượt là hình chiếu vuông góc của M lên
lần lượt là hình chiếu vuông góc của M lên ![]() . Khi đó
. Khi đó ![]() với
với ![]()
- Để tìm tọa độ điểm A ta đi tìm tọa độ vectơ
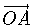
- Nếu biết tọa độ hai điểm
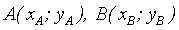 suy ra tọa độ
suy ra tọa độ  được xác định theo công
được xác định theo công
thức ![]()
Chú ý: ![]() nếu
nếu ![]() nằm trên tia
nằm trên tia ![]() (hoặc
(hoặc ![]() ) và
) và ![]() nếu H nằm trên tia đối tia
nếu H nằm trên tia đối tia ![]() (hoặc
(hoặc ![]() ).
).
A. VÍ DỤ MINH HỌA
Ví dụ 1: Trong mặt phẳng tọa độ ![]() . Cho điểm
. Cho điểm ![]() . Tìm tọa độ của các điểm
. Tìm tọa độ của các điểm ![]() đối xứng với
đối xứng với ![]() qua trục hoành?
qua trục hoành?
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Lời giải
Chọn A.
![]() đối xứng với
đối xứng với ![]() qua trục hoành suy ra
qua trục hoành suy ra ![]() .
.
Ví dụ 2:Vectơ ![]() được phân tích theo hai vectơ đơn vị như thế nào?
được phân tích theo hai vectơ đơn vị như thế nào?
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Lời giải
Chọn D
Ta có: ![]() .
.
Ví dụ 3:Mệnh đề nào sau đây đúng?
A. Hai vectơ ![]() đối nhau.
đối nhau.
B. Hai vectơ ![]() đối nhau.
đối nhau.
C. Hai vectơ ![]() đối nhau.
đối nhau.
D. Hai vectơ ![]() đối nhau.
đối nhau.
Lời giải
Chọn C
Ta có: ![]() và
và ![]() đối nhau.
đối nhau.
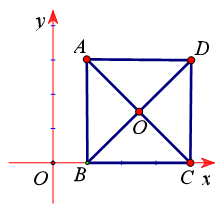
Ví dụ 4:Trong hệ trục tọa độ ![]() , cho hình vuông
, cho hình vuông ![]() tâm I và có
tâm I và có ![]() . Biết điểm
. Biết điểm ![]() thuộc trục
thuộc trục ![]() và
và ![]() cùng hướng với
cùng hướng với ![]() . Tìm tọa độ các vectơ
. Tìm tọa độ các vectơ ![]() ?
?
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Lời giải
Chọn C.
Từ giả thiết ta xác định được hình vuông trên mặt
phẳng tọa độ ![]() như hình vẽ bên.
như hình vẽ bên.
Vì điểm ![]() suy ra
suy ra ![]()
Do đó ![]()
Vậy ![]()
Ví dụ 5: Trong mặt phẳng tọa độ ![]() . Cho hình thoi
. Cho hình thoi ![]() cạnh a và
cạnh a và ![]() . Biết
. Biết ![]() trùng với gốc tọa độ
trùng với gốc tọa độ ![]() ;
; ![]() thuộc trục
thuộc trục ![]() và
và ![]() . Tìm tọa độ các đỉnh
. Tìm tọa độ các đỉnh ![]() và
và ![]() của hình thoi
của hình thoi ![]() .
.
A.  . B.
. B.  .
.
C. 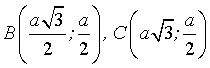 . D.
. D.  .
.

Lời giải
Chọn A.
Từ giả thiết ta xác định được hình thoi trên mặt phẳng tọa độ
![]()
Gọi I là tâm hình thoi ta có 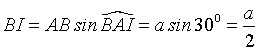

Suy ra 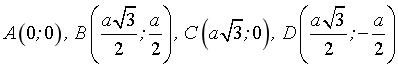 .
.
B. BÀI TẬP TỰ LUYỆN
- Trong mặt phẳng tọa độ
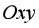 . Cho điểm
. Cho điểm  . Tìm tọa độ của các điểm
. Tìm tọa độ của các điểm  đối xứng với
đối xứng với 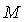 qua trục tung?
qua trục tung?
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
- Trong hệ trục tọa độ
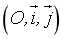 , cho tam giác đều
, cho tam giác đều  cạnh
cạnh  , biết
, biết 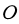 là trung điểm
là trung điểm  ,
,  cùng hướng với
cùng hướng với 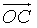 ,
, 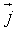 cùng hướng
cùng hướng  . Tìm tọa độ của các đỉnh của tam giác
. Tìm tọa độ của các đỉnh của tam giác 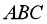 .
. 
- Trong hệ trục tọa độ
 , cho tam giác đều
, cho tam giác đều  cạnh
cạnh 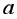 , biết
, biết 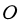 là trung điểm
là trung điểm  ,
,  cùng hướng với
cùng hướng với  ,
,  cùng hướng
cùng hướng  . Tìm tọa độ tâm đường tròn ngoại tiếp tam giác
. Tìm tọa độ tâm đường tròn ngoại tiếp tam giác  .
.
Lời giải
Tâm đường tròn ngoại tiếp tam giác đều trùng với trọng tâm 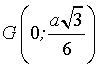
- Trong hệ trục tọa độ
 , cho hình thoi
, cho hình thoi  tâm O có
tâm O có 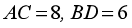 . Biết
. Biết  và
và 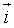 cùng hướng,
cùng hướng,  và
và  cùng hướng. Tính tọa độ trọng tâm tam giác
cùng hướng. Tính tọa độ trọng tâm tam giác 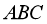
Lời giải
![]() .
.
- Cho hình bình hành
 có
có 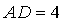 và chiều cao ứng với cạnh
và chiều cao ứng với cạnh  ,
,  . Chọn hệ trục tọa độ
. Chọn hệ trục tọa độ  sao cho
sao cho  và
và  cùng hướng,
cùng hướng,  . Tìm tọa độ các vecto
. Tìm tọa độ các vecto 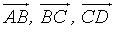 và
và 
- Cho lục giác đều
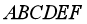 . Chọn hệ trục tọa độ
. Chọn hệ trục tọa độ  , trong đó
, trong đó  là tâm lục giác đều ,
là tâm lục giác đều , 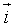 cùng hướng với
cùng hướng với  ,
,  cùng hướng
cùng hướng  . Tính tọa độ các đỉnh lục giác đều , biết cạnh của lục giác là
. Tính tọa độ các đỉnh lục giác đều , biết cạnh của lục giác là  .
.
Lời giải
ĐS: ![]()
![]()