DẤU CỦA NHỊ THỨC BẬC NHẤT
I – LÝ THUYẾT
1. Nhị thức bậc nhất
Nhị thức bậc nhất đối với ![]() là biểu thức dạng
là biểu thức dạng ![]() trong đó
trong đó ![]() là hai số đã cho,
là hai số đã cho, ![]() .
.
2. Dấu của nhị thức bậc nhất
Định lí. Nhị thức ![]() có giá trị cùng dấu với hệ số
có giá trị cùng dấu với hệ số ![]() khi
khi ![]() lấy các giá trị trong khoảng
lấy các giá trị trong khoảng  trái dấu với hệ số
trái dấu với hệ số ![]() khi
khi ![]() lấy giá trị trong khoảng
lấy giá trị trong khoảng 
a. Sử dụng bảng xét dấu (phải cùng – trái trái: với hệ số a)
|
|
|
|
|
|
|
|
|
|
|
|
b. Sử dụng trục số
● Nếu ![]() thì :
thì :

● Nếu ![]() thì :
thì :

● Minh họa bằng đồ thị

3. Một số ứng dụng.
a) Bất phương trình tích
· Dạng: ![]() (1) (trong đó
(1) (trong đó ![]() ,
, ![]() là những nhị thức bậc nhất.)
là những nhị thức bậc nhất.)
· Cách giải: Lập bảng xét dấu của ![]() . Từ đó suy ra tập nghiệm của (1).
. Từ đó suy ra tập nghiệm của (1).
b) Bất phương trình chứa ẩn ở mẫu
· Dạng: 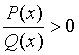 (2) (trong đó
(2) (trong đó ![]() ,
, ![]() là những nhị thức bậc nhất.)
là những nhị thức bậc nhất.)
· Cách giải: Lập bảng xét dấu của ![]() . Từ đó suy ra tập nghiệm của (2).
. Từ đó suy ra tập nghiệm của (2).
Chú ý. Không nên qui đồng và khử mẫu.
c) Bất phương trình chứa ẩn trong dấu GTTĐ
· Tương tự như giải phương trình chứa ẩn trong dấu GTTĐ, ta thường sử dụng định nghĩa hoặc tính chất của GTTĐ để khử dấu GTTĐ.
· Dạng 1: 
· Dạng 2: 
Chú ý. Với B > 0 ta có: ![]() ;
; 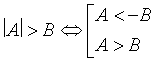 .
.
II – DẠNG TOÁN
1. Dạng 1: Xét dấu của nhị thức bậc nhất
A. VÍ DỤ MINH HỌA
Ví dụ 1: Cho nhị thức bậc nhất ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A. ![]() với
với ![]() . B.
. B. ![]() với
với  .
.
C. ![]() với
với  . D.
. D. ![]() với
với 
Hướng dẫn giải
Chọn D.
Ta có 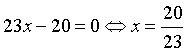 ,
, ![]() .
.
Bảng xét dấu
|
|
|
|
|
|
Vậy ![]() với
với 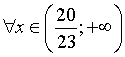 .
.
Ví dụ 2: Các số tự nhiên bé hơn ![]() để
để  luôn âm
luôn âm
A. ![]() . B.
. B.  .
.
C. ![]() . D.
. D. ![]()
Hướng dẫn giải
Chọn C.
Ta có 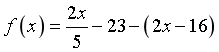
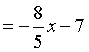
 ,
,  .
.
Bảng xét dấu
|
|
|
|
|
+ |
![]() với
với  .
.
Vậy ![]() .
.
Ví dụ 3: Với ![]() thuộc tập hợp nào dưới đây thì
thuộc tập hợp nào dưới đây thì 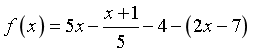 luôn âm
luôn âm
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Chọn C.
Ta có 

![]() ,
, 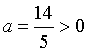 .
.
Bảng xét dấu
|
|
|
|
|
|
![]() với
với ![]() .
.
Vậy ![]() .
.
Ví dụ 4: Tìm tất cả các giá trị thực của tham số ![]() để
để ![]() không âm với mọi
không âm với mọi ![]()
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Chọn C.
![]() .
. ![]()
+ Xét ![]() . (không thỏa)
. (không thỏa)
+ Xét ![]() thì
thì ![]() không thỏa điều kiện nghiệm đã cho.
không thỏa điều kiện nghiệm đã cho.
+ Xét ![]() thì
thì ![]() thỏa điều kiện nghiệm đã cho.
thỏa điều kiện nghiệm đã cho.
Vậy ![]() .
.
Ví dụ 5: Gọi ![]() là tập tất cả các giá trị của
là tập tất cả các giá trị của ![]() để
để ![]() luôn âm khi
luôn âm khi ![]() . Hỏi các tập hợp nào sau đây là phần bù của tập
. Hỏi các tập hợp nào sau đây là phần bù của tập ![]() ?
?
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Chọn D.
![]()
![]()
![]() (do
(do ![]() )
)
Vậy ![]()
![]() .
.

