TỔNG VÀ HIỆU CỦA HAI VECTƠ
I – LÝ THUYẾT
1. Tổng của hai vectơ
Định nghĩa: Phép cộng hai vectơ ![]() và
và ![]() là vectơ
là vectơ ![]() , được xác định tùy theo vị trí của hai vectơ. Có 3 trường hợp.
, được xác định tùy theo vị trí của hai vectơ. Có 3 trường hợp.

Quy tắc 3 điểm |

Quy tắc hình bình hành |

2 trường hợp trên |
– Quy tắc ba điểm: Với ba điểm bất kỳ ![]() ta có
ta có ![]()
– Quy tắc hình bình hành: Cho ![]() là hình bình hành khi đó ta có
là hình bình hành khi đó ta có  và
và 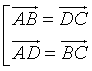
Tính chất:
| – Giao hoán: |
– Kết hợp: |
| – Cộng với vectơ đối: |
– Cộng với vectơ không: |
2. Hiệu của hai vectơ
Vectơ đối của vectơ ![]() kí hiệu là –
kí hiệu là – ![]() . Đặc biệt
. Đặc biệt ![]()
Định nghĩa: Hiệu hai vectơ ![]() và
và ![]() là vectơ
là vectơ ![]()
Tính chất: + ![]() +
+ ![]() +
+ ![]()
Quy tắc tam giác đối với hiệu hai vectơ
Với ba điểm bất kì ![]() ta có
ta có ![]()
3. Trung điểm của đoạn thẳng và trọng tâm tam giác
- Điểm I là trung điểm của đoạn

- Điểm G là trọng tâm

2. Dạng 2: Tìm vectơ đối và hiệu của 2 vectơ
Phương pháp giải:
– Áp dùng định nghĩa: Tìm vectơ đối, tính tổng
– Áp dụng quy tắc 3 điểm, hình bình hành và tính chất
Ví dụ 1: Cho ![]() và
và ![]() là các vectơ khác
là các vectơ khác ![]() với
với ![]() là vectơ đối của
là vectơ đối của ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
A. Hai vectơ ![]() cùng phương. B. Hai vectơ
cùng phương. B. Hai vectơ ![]() ngược hướng.
ngược hướng.
C. Hai vectơ ![]() cùng độ dài. D. Hai vectơ
cùng độ dài. D. Hai vectơ ![]() chung điểm đầu.
chung điểm đầu.
Lời giải.
Chọn D.
Ta có ![]() . Do đó,
. Do đó, ![]() và
và ![]() cùng phương, cùng độ dài và ngược hướng nhau.
cùng phương, cùng độ dài và ngược hướng nhau.
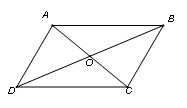
Ví dụ 2. Gọi ![]() là tâm hình bình hành
là tâm hình bình hành ![]() . Đẳng thức nào sau đây sai?
. Đẳng thức nào sau đây sai?
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Lời giải.
Chọn B. Xét các đáp án:
| Đáp án A. Ta có Đáp án B. Ta có Đáp án C. Ta có Đáp án D. Ta có |
 |
Ví dụ 3. Gọi ![]() là tâm hình vuông
là tâm hình vuông ![]() . Tính
. Tính ![]() .
.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Lời giải.
Chọn B. Ta có ![]() .
.
Ví dụ 4. Cho ![]() là tâm hình bình hành
là tâm hình bình hành ![]() . Hỏi vectơ
. Hỏi vectơ ![]() bằng vectơ nào?
bằng vectơ nào?
 A.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Lời giải.
Chọn B. Ta có ![]() .
.
3. Dạng 3: Tính độ dài của vectơ
Phương pháp giải:
– Biến đổi vectơ tổng, vectơ hiệu thành một vectơ duy nhất.
– Tính độ dài của vectơ đó.
– Từ đó suy ra độ dài của vectơ tổng, vectơ hiệu.
A. VÍ DỤ MINH HỌA
Ví dụ 1: Cho tam giác ![]() đều cạnh
đều cạnh ![]() . Khi đó
. Khi đó ![]() bằng:
bằng:
A. ![]() B.
B. ![]()
C. ![]() D. Một đáp án khác.
D. Một đáp án khác.
Lời giải.
Chọn A
| Gọi Suy ra Ta lại có |
 |
Ví dụ 2. Cho tam giác vuông cân ![]() tại
tại ![]() có
có ![]() . Tính
. Tính ![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Lời giải.
| Chọn A. Gọi
|
 |
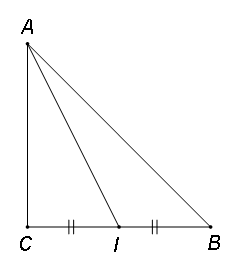
Ví dụ 3. Cho tam giác ![]() vuông cân đỉnh
vuông cân đỉnh ![]() ,
, ![]() . Tính độ dài của
. Tính độ dài của ![]()
A. ![]() B.
B. ![]()
 C.
C. ![]() D.
D. ![]()
Lời giải.
Chọn A.
Ta có ![]()
Gọi ![]() là trung điểm
là trung điểm ![]()
Khi đó ![]()
B. BÀI TẬP TỰ LUYỆN
NHẬN BIẾT
- Cho 4 điểm bất kì
 . Đẳng thức nào sau đây đúng?
. Đẳng thức nào sau đây đúng?
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
- Cho hai điểm phân biệt
 . Điều kiện để điểm
. Điều kiện để điểm 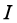 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 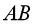 là:
là:
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
- Cho ba điểm phân biệt
 . Đẳng thức nào sau đây là đúng?
. Đẳng thức nào sau đây là đúng?
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
- Chọn khẳng định sai:
A. Nếu ![]() là trung điểm đoạn
là trung điểm đoạn ![]() thì
thì ![]() .
.
B. Nếu ![]() là trung điểm đoạn
là trung điểm đoạn ![]() thì
thì ![]() .
.
C. Nếu ![]() là trung điểm đoạn
là trung điểm đoạn ![]() thì
thì ![]() .
.
D. Nếu ![]() là trung điểm đoạn
là trung điểm đoạn ![]() thì
thì ![]() .
.
- Cho hình bình hành
 . Đẳng thức nào sau đây sai ?
. Đẳng thức nào sau đây sai ?
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
- Cho 4 điểm bất kỳ
 . Đẳng thức nào sau đây là đúng:
. Đẳng thức nào sau đây là đúng:
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
- Cho tam giác
 , khẳng định nào sau là đúng?
, khẳng định nào sau là đúng?
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
- Cho ba vectơ
 đều khác vectơ – không. Trong đó hai vectơ
đều khác vectơ – không. Trong đó hai vectơ 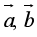 cùng hướng, hai vectơ
cùng hướng, hai vectơ  đối nhau. Khẳng định nào sau đây đúng ?
đối nhau. Khẳng định nào sau đây đúng ?
A. Hai vectơ ![]() cùng hướng.
cùng hướng.
B. Hai vectơ ![]() ngược hướng.
ngược hướng.
C. Hai vectơ ![]() đối nhau.
đối nhau.
D. Hai vectơ ![]() bằng nhau.
bằng nhau.
- Cho các điểm phân biệt
 . Đẳng thức nào sau đây sai
. Đẳng thức nào sau đây sai
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
- Gọi
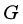 là trọng tâm tam giác vuông
là trọng tâm tam giác vuông  với cạnh huyền
với cạnh huyền  . Vectơ
. Vectơ  có độ dài bằng bao nhiêu?
có độ dài bằng bao nhiêu?
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
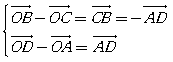 . Vậy B sai.
. Vậy B sai. . Vậy D đúng.
. Vậy D đúng.