ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC
A – TÓM TẮT LÝ THUYẾT
|
1. Giới hạn lượng giác · 2. Đạo hàm các hàm số lượng giác
|
B – BÀI TẬP
DẠNG 1: TÍNH ĐẠO HÀM TẠI MỘT ĐIỂM BẰNG CÔNG THỨC HOẶC BẰNG MTCT
Câu 1. Hàm số 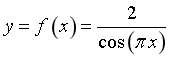 có
có ![]() bằng:
bằng:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải:
Chọn D.
 .
.
 .
.
Câu 2. Cho hàm số ![]() Tính
Tính 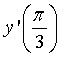 bằng:
bằng:
A.  . B.
. B.  . C.
. C. 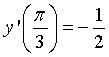 . D.
. D.  .
.
Hướng dẫn giải:
Chọn B.
![]() .
.
 .
.
Câu 3. Cho hàm số 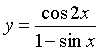 . Tính
. Tính  bằng:
bằng:
A.  . B.
. B. 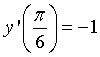 . C.
. C.  . D.
. D.  .
.
Hướng dẫn giải:
Chọn D.
 .
.
 .
.
Câu 4. Cho hàm số ![]() . Giá trị
. Giá trị  bằng:
bằng:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải:
Chọn A.
 .
.
 .
.
Câu 5. Cho hàm số ![]() . Giá trị
. Giá trị  bằng:
bằng:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải:
Chọn C.
 .
.
 .
.

Câu 6. Cho hàm số  . Giá trị
. Giá trị  bằng:
bằng:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D. Không tồn tại.
. D. Không tồn tại.
Hướng dẫn giải:
Chọn C.
 .
.
 .
.
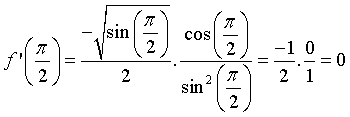 .
.
Câu 7. Xét hàm số  . Tính giá trị
. Tính giá trị 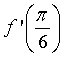 bằng:
bằng:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải:
Chọn D.
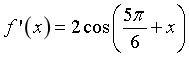 .
.
 .
.
Câu 8. Cho hàm số  . Giá trị
. Giá trị ![]() bằng:
bằng:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải:
Chọn A.
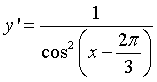 .
.
![]() .
.
Câu 9. Cho hàm số 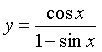 . Tính
. Tính 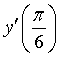 bằng:
bằng:
A.  . B.
. B. 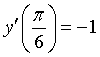 . C.
. C. 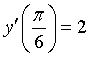 . D.
. D.  .
.
Hướng dẫn giải:
Chọn D.
Ta có 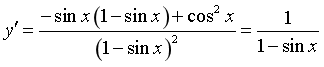 .
.
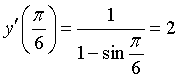 .
.
Câu 10. Cho hàm số  . Giá trị
. Giá trị  là:
là:
A. ![]() B.
B. ![]() C.
C. ![]() D. Không tồn tại.
D. Không tồn tại.
Hướng dẫn giải:
Chọn C.

 ;
;  (với
(với 


