ĐẠO HÀM

Vietlearn
4 minutes

A. LÝ THUYẾT CHUNG

1. Định nghĩa đạo hàm tại một điểm

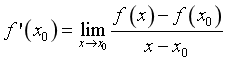1.1. Định nghĩa : Cho hàm số IMG_256 xác định trên khoảng IMG_257 và IMG_258 , đạo hàm của hàm số tại điểm IMG_259 là : IMG_260 .

1.2. Chú ý :

· Nếu kí hiệu IMG_261 thì :
IMG_262 .

· Nếu hàm số IMG_263 có đạo hàm tại IMG_264 thì nó liên tục tại điểm đó.

2. Ý nghĩa của đạo hàm

2.1. Ý nghĩa hình học: Cho hàm số IMG_265 có đồ thị IMG_266

· IMG_267 là hệ số góc của tiếp tuyến đồ thị IMG_268 của hàm số IMG_269 tại IMG_270 .

· Phương trình tiếp tuyến của đồ thị hàm số IMG_271 tại điểm IMG_272 là :
IMG_273 .

2.2. Ý nghĩa vật lí :

· Vận tốc tức thời của chuyển động thẳng xác định bởi phương trình : IMG_274 tại thời điểm IMG_275 là IMG_276.

· Cường độ tức thời của điện lượng IMG_277 tại thời điểm IMG_278 là : IMG_279 .

3. Qui tắc tính đạo hàm và công thức tính đạo hàm

3.1. Các quy tắc : Cho IMG_280 là hằng số .

· IMG_281

· IMG_282

· IMG_283

· Nếu IMG_284 .

3.2. Các công thức :

· IMG_285

· IMG_286

· IMG_287

· IMG_288

· IMG_289

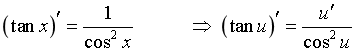
· IMG_290

· IMG_291 .

4. Vi phân

4.1. Định nghĩa :

· Cho hàm số IMG_292 có đạo hàm tại IMG_293 vi phân của hàm số IMG_294 tại điểm IMG_295 là :
IMG_296 .

· Cho hàm số IMG_297 có đạo hàm IMG_298 thì tích IMG_299 được gọi là vi phân của hàm số IMG_300 . Kí hiệu : IMG_301 hay IMG_302 .

4.2. Công thức tính gần đúng :
IMG_303 .

5. Đạo hàm cấp cao

5.1. Đạo hàm cấp 2 :

Tại sao có đoàn tàu trên không chạy ở hai bên dầm thép?

· Định nghĩa : IMG_304

· Ý nghĩa cơ học: Gia tốc tức thời của chuyển động IMG_305 tại thời điểm IMG_306 là IMG_307.

5.2. Đạo hàm cấp cao : IMG_308 .

B. BÀI TẬP

TÍNH ĐẠO HÀM

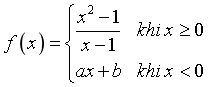Câu 1: Tìm IMG_309 để hàm số IMG_310 có đạo hàm tại điểm IMG_311 .

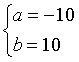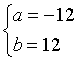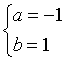A. IMG_312 . B. IMG_313 . C. IMG_314 . D. IMG_315 .

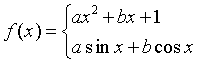
Câu 2: Tìm IMG_316 để hàm số IMG_317 IMG_318 có đạo hàm tại điểm IMG_319

A. IMG_320 . B. IMG_321 . C. IMG_322 . D. IMG_323 .

Câu 3: Cho hàm số IMG_324 . Tính IMG_325 .

A. IMG_326 . B. IMG_327 . C. IMG_328 . D. IMG_329 .

Câu 4: Cho hàm số IMG_330 IMG_331 .Giá trị của IMG_332 bằng:

A. IMG_333 . B. IMG_334 . C. IMG_335 . D. Không tồn tại.

Câu 5: Với hàm số IMG_336 IMG_337 .Để tìm đạo hàm IMG_338 một học sinh lập luận qua các bước như sau:

1. IMG_339 .

2.Khi IMG_340 thì IMG_341 nên IMG_342 .

3.Do IMG_343 nên hàm số liên tục tại IMG_344 .

4.Từ IMG_345 liên tục tại IMG_346 có đạo hàm tại IMG_347 .

Lập luận trên nếu sai thì bắt đầu từ bước:

A. Bước 1. B. Bước 2. C. Bước 3. D. Bước 4.

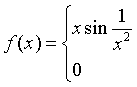
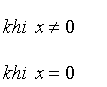Câu 6: Cho hàm số IMG_348 IMG_349 .

IMG_350 Hàm số IMG_351 liên tục tại điểm IMG_352 .

IMG_353 Hàm số IMG_354 không có đạo hàm tại điểm IMG_355 .

Trong các mệnh đề trên:

A. Chỉ IMG_356 đúng. B. Chỉ IMG_357 đúng. C. Cả IMG_358 đều đúng. D. Cả IMG_359 đều sai.

Câu 7: Cho hàm số 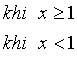IMG_360 IMG_361 .Tìm IMG_362 để hàm số có đạo hàm tại IMG_363

A. IMG_364 . B. IMG_365 . C. IMG_366 . D. IMG_367 .

Câu 8: Đạo hàm của hàm số IMG_368 là:

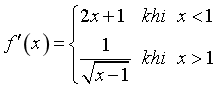A. IMG_369 . B. IMG_370 .

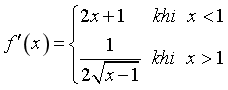C. IMG_371 . D. IMG_372 .

Câu 9: Cho hàm số IMG_373 . Tìm IMG_374 , IMG_375 để hàm số IMG_376 có đạo hàm trên IMG_377 .

A. IMG_378 , IMG_379 . B. IMG_380 , IMG_381 . C. IMG_382 , IMG_383 . D. IMG_384 , IMG_385 .

Câu 10: Đạo hàm của hàm số IMG_386 bằng biểu thức có dạng IMG_387 . Khi đó IMG_388 bằng:

A. 0. B. 2. C. 3. D. 5.

MÔN SINH HỌC – LỚP 11 | ÔN TẬP CHƯƠNG II