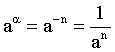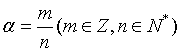A – LÝ THUYẾT CHUNG

I. LŨY THỪA

1. Định nghĩa luỹ thừa

Số mũ a	Cơ số a	Luỹ thừa
	a Î R	(n thừa số a)

2. Tính chất của luỹ thừa

· Với mọi a > 0, b > 0 ta có:

· a > 1 : ; 0 < a < 1 :

· Với 0 < a < b ta có:

;

Chú ý: + Khi xét luỹ thừa với số mũ 0 và số mũ nguyên âm thì cơ số a phải khác 0.

+ Khi xét luỹ thừa với số mũ không nguyên thì cơ số a phải dương.

3. Định nghĩa và tính chất của căn thức

· Căn bậc n của a là số b sao cho .

· Với a, b ³ 0, m, n Î N*, p, q Î Z ta có:

; ; ;

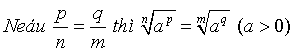; Đặc biệt

· Nếu n là số nguyên dương lẻ và a < b thì .

Nếu n là số nguyên dương chẵn và 0 < a < b thì .

Chú ý:

+ Khi n lẻ, mỗi số thực a chỉ có một căn bậc n. Kí hiệu .

+ Khi n chẵn, mỗi số thực dương a có đúng hai căn bậc n là hai số đối nhau.

II. HÀM SỐ LŨY THỪA

1) Hàm số luỹ thừa (a là hằng số)

 

Số mũ a	Hàm số	Tập xác định D
a = n (n nguyên dương)		D = R
a = n (n nguyên âm hoặc n = 0)		D = R \ {0}
a là số thực không nguyên		D = (0; +¥)

Chú ý: Hàm số không đồng nhất với hàm số .

2) Đạo hàm

· ;

Chú ý: .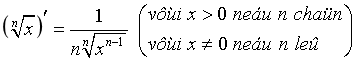

III. LÔGARIT

1. Định nghĩa

· Với a > 0, a ¹ 1, b > 0 ta có:

Chú ý: có nghĩa khi

· Logarit thập phân:

· Logarit tự nhiên (logarit Nepe): (với )

2. Tính chất

· ; ; ;

· Cho a > 0, a ¹ 1, b, c > 0. Khi đó:

+ Nếu a > 1 thì

+ Nếu 0 < a < 1 thì

3. Các qui tắc tính logarit

Với a > 0, a ¹ 1, b, c > 0, ta có:

· · ·

4. Đổi cơ số

Với a, b, c > 0 và a, b ¹ 1, ta có:

· hay

· ·

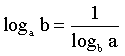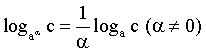
IV. HÀM SỐ MŨ, HÀM SỐ LÔGARIT

 

1) Hàm số mũ (a > 0, a ¹ 1).

· Tập xác định: D = R.

· Tập giá trị: T = (0; +¥).

· Khi a > 1 hàm số đồng biến, khi 0 < a < 1 hàm số nghịch biến.

· Nhận trục hoành làm tiệm cận ngang.

· Đồ thị:

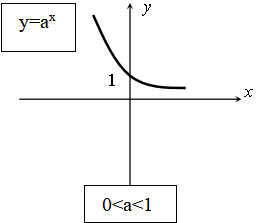
2) Hàm số logarit (a > 0, a ¹ 1)

· Tập xác định: D = (0; +¥).

· Tập giá trị: T = R.

· Khi a > 1 hàm số đồng biến, khi 0 < a < 1 hàm số nghịch biến.

· Nhận trục tung làm tiệm cận đứng.

· Đồ thị:

3) Giới hạn đặc biệt

· · ·

4) Đạo hàm

 

· ;

;

 

· ;

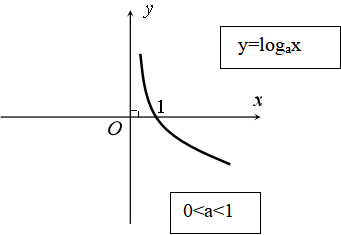
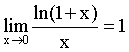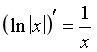(x > 0);

B – BÀI TẬP TRẮC NGHIỆM

Câu 1: Cho , và , trong đó là các số nguyên. Tính giá trị biểu thức

A. . B. C. D.

Câu 2: Nếu và thì giá trị của bằng

A. B. C. D.

Câu 3: Với , cho biết: . Chọn khẳng định đúng:

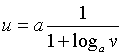A. . B. . C. . D. .

Câu 4: Trong hình vẽ dưới đây có đồ thị của các hàm số , , .

.

Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?

A. B. C. D.

Câu 5: Cho bốn hàm số , , 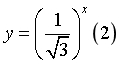, có đồ thị là đường cong theo phía trên đồ thị, thứ tự từ trái qua phải là như hình vẽ bên.

Tương ứng hàm số – đồ thị đúng là

A. .

B.

C. .

D.