TÌM ĐIỀU KIỆN ĐỂ HÀM SỐ CÓ CỰC TRỊ THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC

Phương pháp . Tiến hành theo các bước sau:

Bước 1. Tìm tập xác định của hàm số f.

Bước 2. Tính .

Bước 3.Sử dụng định lí sau: “ Nếu hàm số f có đạo hàm liên tục trên (a,b) và .Thế thì điểm là điểm cực trị của hàm số f nếu và chỉ nếu đạo hàm đổi dấu khi x đi qua ”.

Bước 4.Giải quyết yêu cầu của cực trị (nếu có).

Chú ý:

* Nếu ta gặp biểu thức đối xứng của hoành độ các điểm cực trị và hoành độ các điểm cực trị là nghiệm của một tam thức bậc hai thì ta sử dụng định lí Viét.

* Khi tính giá trị cực trị của hàm số qua điểm cực trị ta thường dùng các kết quả sau:

Định lí 1: Cho hàm đa thức , giả sử khi đó nếu là điểm cực trị của hàm số thì giá trị cực trị của hàm số là: và gọi là phương trình quỹ tích của các điểm cực trị.
Chứng minh: Giả sử là điểm cực trị của hàm số, vì là hàm đa thức nên (đpcm) .

Định lí 2: Cho hàm phân thức hữu tỉ 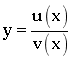khi đó nếu là điểm cực

trị của hàm số thì giá trị cực trị của hàm số: .

Và là phương trình quỹ tích của các điểm cực trị.

Chứng minh: Ta có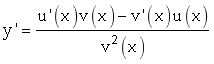

. Giả sử là điểm cực trị của hàm số thì là nghiệm của phương trình .

Bài toán 01:

TÌM ĐIỀU KIỆN ĐỂ HÀM SỐ CÓ CỰC TRỊ CÙNG DẤU, TRÁI DẤU.

Phương pháp .

Giả sử

Hàm số có hai điểm cực trị dương có hai nghiệm dương phân biệt : .

Hàm số có hai điểm cực trị âm có hai nghiệm âm phân biệt

.

Hàm số có hai điểm cực trị trái dấu có hai nghiệm trái dấu

.

Hàm số có hai cực trị có giá trị cực trị cùng dấu .

Ví dụ : Định m để hàm số có cực trị trái dấu .

Lời giải.

Hàm số đã cho xác định

Ta có:

Hàm số có cực trị trái dấu nhau khi và chỉ khi có hai nghiệm phân biệt thỏa mãn

Vậy, với thì hàm số có cực trị trái dấu nhau .

CÁC BÀI TOÁN LUYỆN TẬP

Bài 1: Tìm m để hàm số :

1. 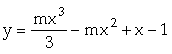có hai điểm cực trị và hai giá trị cực trị cùng dấu.

2. đạt cực đại và cực tiểu đồng thời hai giá trị cực trị cùng dấu.

3. có hai cực trị trái dấu.

Bài 2: Tìm m để hàm số :

1. 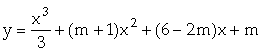đạt cực trị tại hai điểm trái dấu.

2. có các điểm cực đại, cực tiểu. Chứng minh rằng khi đó hai điểm cực trị luôn cách đều đường thẳng .

3. có cực đại và cực tiểu đồng thời giá trị cực đại và cực tiểu của hàm số trái dấu nhau.

Bài toán 02: TÌM ĐIỀU KIỆN ĐỂ HÀM SỐ CÓ CỰC ĐẠI, CỰC TIỂU NẰM VỀ MỘT PHÍA, HAI PHÍA CỦA HỆ TRỤC TỌA ĐỘ.

Phương pháp .

Giả sử

Hàm số có hai cực trị nằm về phía đối với tung .

Hàm số có hai cực trị nằm về phía đối với trục tung .

Hàm số có hai cực trị nằm trên trục hoành .

Hàm số có hai cực trị nằm dưới trục hoành .

Hàm số có cực trị tiếp xúc với trục hoành .

Các ví dụ

Ví dụ 1 : Cho hàm số ( là tham số) có đồ thị là Xác định để có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.

Lời giải.

Hàm số đã cho xác định

Phương trình hoành độ giao điểm của và trục hoành:

hoặc

có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành khi có nghiệm phân biệt tức phương trình có nghiệm phân biệt khác

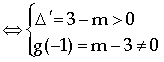
Vậy, với thì hàm số có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.

Ví dụ 2 : Cho hàm số ( là tham số) có đồ thị là Xác định để có các điểm cực đại, cực tiểu nằm về cùng một phía đối với trục tung.

Lời giải.

Hàm số đã cho xác định

Ta có:

Đồ thị có điểm cực đại và cực tiểu nằm cùng phía đối với trục tung Û có nghiệm phân biệt cùng dấu Û

Vậy, với thì hàm số có các điểm cực đại, cực tiểu nằm về cùng một phía đối với trục tung.