TIẾP TUYẾN CỦA HÀM SỐ
· Ý nghĩa hình học của đạo hàm: Đạo hàm của hàm số ![]() tại điểm
tại điểm ![]() là hệ số góc
là hệ số góc
của tiếp tuyến với đồ thị (C) của hàm số tại điểm ![]() .
.
Khi đó phương trình tiếp tuyến của (C) tại điểm ![]() là:
là:
![]()
![]()
· Điều kiện cần và đủ để hai đường ![]() và
và ![]() tiếp xúc nhau
tiếp xúc nhau
tại điểm có hoành độ ![]() là hệ phương trình
là hệ phương trình 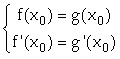 có nghiệm
có nghiệm ![]()
Nghiệm của hệ là hoành độ của tiếp điểm của hai đường đó.
· Nếu ![]() và
và ![]() thì
thì
![]() và
và ![]() iếp xúc nhau Û phương trình
iếp xúc nhau Û phương trình ![]() có nghiệm kép.
có nghiệm kép.
Các dạng tiếp tuyến của đồ thị hàm số thường gặp
– Viết phương trình tiếp tuyến khi biết tọa độ tiếp điểm ![]() , hoặc hoành độ
, hoặc hoành độ ![]() , hoặc tung độ
, hoặc tung độ ![]() .
.
– Viết phương trình tiếp tuyến khi biết tiếp tuyến đi qua điểm ![]() cho trước.
cho trước.
– Viết phương trình tiếp tuyến khi biết hệ số góc của nó.
Phương pháp:
Cho hàm số ![]() có đồ thị
có đồ thị ![]() và
và ![]() là điểm trên
là điểm trên ![]() . Tiếp tuyến với đồ thị
. Tiếp tuyến với đồ thị ![]() tại
tại ![]() có:
có:
– Hệ số góc: ![]()
– Phương trình: ![]() , hay
, hay ![]()
Vậy, để viết được phương trình tiếp tuyến tại ![]() chúng ta cần đủ ba yếu tố sau:
chúng ta cần đủ ba yếu tố sau:
– Hoành độ tiếp điểm: ![]()
– Tung độ tiếp điểm: ![]() (Nếu đề chưa cho, ta phải tính bằng cách thay
(Nếu đề chưa cho, ta phải tính bằng cách thay ![]() vào hàm số
vào hàm số ![]() )
)
– Hệ số góc ![]()
B. LUYỆN KĨ NĂNG GIẢI CÁC DẠNG BÀI TẬP.
Phương pháp .
1. Hai đồ thị tiếp xúc
1.1. Định nghĩa: Hai đồ thị của hai hàm số ![]() và
và ![]() gọi là tiếp xúc nhau tại điểm M nếu tại M chúng có cùng tiếp tuyến.
gọi là tiếp xúc nhau tại điểm M nếu tại M chúng có cùng tiếp tuyến.
2.1. Định lí 1: Hai đồ thị của hai hàm số ![]() và
và ![]() tiếp xúc nhau khi và chỉ khi hệ phương trình:
tiếp xúc nhau khi và chỉ khi hệ phương trình:  có nghiệm và nghiệm của hệ là tọa độ tiếp điểm.
có nghiệm và nghiệm của hệ là tọa độ tiếp điểm.
2. Tiếp tuyến của đồ thị hàm số
1.2. Định nghĩa: Cho hàm số ![]() . Một cát tuyến
. Một cát tuyến ![]() được giới hạn bởi đường thẳng
được giới hạn bởi đường thẳng ![]() khi
khi ![]() dần tới
dần tới ![]() thì
thì ![]() gọi là tiếp tuyến của đồ thị.
gọi là tiếp tuyến của đồ thị. ![]() gọi là tiếp điểm.
gọi là tiếp điểm.
Định lí 2: Đạo hàm của ![]() tại
tại ![]() là hệ số góc của tiếp tuyến tại
là hệ số góc của tiếp tuyến tại ![]() .
.
Nhận xét: Hệ số góc của mọi tiếp tuyến đều có dạng ![]() .
.
2.2. Các bài toán về phương trình tiếp tuyến:
Bài toán 1: Viết phương trình tiếp tuyến của đồ thị hàm số ![]() tại điểm
tại điểm ![]() .
.
Phương pháp:
Tiếp tuyến của đồ thị hàm số ![]() tại
tại ![]() là:
là:
![]() với
với ![]() .
.
Bài toán 2: Viết phương trình tiếp tuyến của đồ thị hàm số ![]() , biết tiếp tuyến có hệ số góc
, biết tiếp tuyến có hệ số góc ![]() .
.
Phương pháp:
Cách 1:
*Phương trình tiếp tuyến có dạng: ![]()
* Điều kiện tiếp xúc là hệ phương trình: 
Từ (2) ta tìm được ![]() , thế vào (1) ta có được
, thế vào (1) ta có được ![]() . Ta có tiếp tuyến cần tìm.
. Ta có tiếp tuyến cần tìm.
Cách 2:
* Giải phương trình ![]() giải phương trình này ta tìm được các nghiệm
giải phương trình này ta tìm được các nghiệm ![]() .
.
* Phương trình tiếp tuyến: ![]() .
.
Chú ý: Đối với bài toán này ta cần lưu ý một số vấn đề sau:
* Số tiếp tuyến của đồ thị chính là số nghiệm của phương trình : ![]() .
.
*Cho hai đường thẳng ![]() và
và ![]() . Khi đó
. Khi đó
i)  , trong đó
, trong đó ![]() .
.
ii) 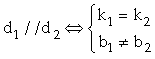
iii) ![]() .
.
Bài toán 01: . Viết phương trình tiếp tuyến khi biết tọa độ tiếp điểm
Phương pháp .
Bài toán 1 :
Hai đường cong ![]() và
và ![]() tiếp xúc nhau tại
tiếp xúc nhau tại ![]() .Khi điểm
.Khi điểm ![]() và tiếp tuyến tại
và tiếp tuyến tại ![]() của
của ![]() trùng với tiếp tuyến tại
trùng với tiếp tuyến tại ![]() của
của ![]() chỉ khi hệ phương trình sau:
chỉ khi hệ phương trình sau: 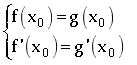 có nghiệm
có nghiệm ![]() .
.
Lưu ý : Mệnh đề sau đây không đúng cho mọi trường hợp:
 tiếp xúc nhau
tiếp xúc nhau ![]() có nghiệm kép .
có nghiệm kép .
Hàm ![]() nhận
nhận ![]() làm nghiệm bội
làm nghiệm bội ![]() nếu
nếu ![]() và
và ![]() . Nghiệm bội lớn hơn hoặc bằng
. Nghiệm bội lớn hơn hoặc bằng ![]() chứ không phải nghiệm kép.
chứ không phải nghiệm kép.
Phép biến đổi tương đương của phương trình nói chung không bảo toàn số bội của nghiệm.
Ví dụ 1. Đường cong ![]() không tiếp xúc với trục hoành tại
không tiếp xúc với trục hoành tại ![]() , tức là phương trình
, tức là phương trình ![]() không nhận
không nhận ![]() làm nghiệm bội lớn hơn hoặc bằng
làm nghiệm bội lớn hơn hoặc bằng ![]() . Khi đó đồ thị
. Khi đó đồ thị ![]() của hàm số tiếp xúc với trục hoành tại
của hàm số tiếp xúc với trục hoành tại ![]() nhưng phương trình
nhưng phương trình ![]() nhận
nhận ![]() làm nghiệm bội
làm nghiệm bội ![]() .
.
Ví dụ 2. Đồ thị ![]() của hàm số tiếp xúc với đường thẳng
của hàm số tiếp xúc với đường thẳng ![]() tại
tại ![]() nhưng phương trình
nhưng phương trình ![]() thì không thể có nghiệm kép.
thì không thể có nghiệm kép.
Như vậy, biến đổi tương đương của phương trình chỉ bảo toàn tập nghiệm, chứ không chắc bảo toàn số bội các nghiệm. Đây cũng là sai lầm dễ mắc phải khi giải quyết bài toán tiếp tuyến.
Bài toán 2 :
![]() Đường cong
Đường cong ![]() có tiếp tuyến tại điểm có hoành độ
có tiếp tuyến tại điểm có hoành độ ![]() khi và chỉ khi hàm số
khi và chỉ khi hàm số ![]() khả vi tại
khả vi tại ![]() . Trong trường hợp
. Trong trường hợp ![]() có tiếp tuyến tại điểm có hoành độ
có tiếp tuyến tại điểm có hoành độ ![]() thì tiếp tuyến đó có hệ số góc
thì tiếp tuyến đó có hệ số góc ![]() .
.
![]() Phương trình tiếp tuyến của đồ thị
Phương trình tiếp tuyến của đồ thị ![]() tại điểm
tại điểm ![]() có dạng :
có dạng : ![]()
Các ví dụ
Ví dụ 1 : Cho hàm số ![]() có đồ thị là (C). Viết phương trình tiếp tuyến của (C) :
có đồ thị là (C). Viết phương trình tiếp tuyến của (C) :
1. Tại điểm ![]() ; 2. Tại điểm có hoành độ bằng 2 ;
; 2. Tại điểm có hoành độ bằng 2 ;
3. Tại điểm có tung độ bằng 1 ;. 4. Tại giao điểm (C) với trục tung ;
5. Có hệ số góc là 9 ;
6. Song song với đường thẳng (d ): ![]() ;
;
7. Vuông góc với đường thẳng (d’ ) : ![]() .
.
Lời giải.
Hàm số đã cho xác định ![]()
Ta có: ![]()
1. Phương trình tiếp tuyến ![]() tại
tại ![]() có phương trình :
có phương trình : ![]()
Ta có: ![]() , khi đó phương trình
, khi đó phương trình ![]() là:
là: ![]()
Chú ý:
Viết phương trình tiếp tuyến của đồ thị hàm số ![]() tại điểm
tại điểm ![]() .
.
Tiếp tuyến của đồ thị hàm số ![]() tại
tại ![]() là:
là: ![]()
2. Thay ![]() vào đồ thị của (C) ta được
vào đồ thị của (C) ta được ![]() .
.
Tương tự câu 1, phương trình ![]() là:
là: ![]()
Chú ý:
Viết phương trình tiếp tuyến của đồ thị hàm số ![]() biết hoành độ tiếp điểm
biết hoành độ tiếp điểm ![]() ,
, ![]()
![]() phương trình tiếp tuyến:
phương trình tiếp tuyến: ![]()
3. Thay ![]() vào đồ thị của (C) ta được
vào đồ thị của (C) ta được ![]() hoặc
hoặc ![]() .
.
Tương tự câu 1, phương trình ![]() là:
là: ![]() ,
, ![]()
Chú ý: Viết phương trình tiếp tuyến của đồ thị hàm số ![]() biết tung độ tiếp điểm bằng
biết tung độ tiếp điểm bằng ![]() . Gọi
. Gọi ![]() là tiếp điểm
là tiếp điểm
Giải phương trình ![]() ta tìm được các nghiệm
ta tìm được các nghiệm ![]() .
.
Tính ![]()
![]() phương trình tiếp tuyến:
phương trình tiếp tuyến: ![]()
4. Trục tung Oy : ![]() .Tương tự câu 1, phương trình
.Tương tự câu 1, phương trình ![]() là:
là: ![]()
5. Gọi ![]() là tọa độ tiếp điểm của đồ thị (C ) của hàm số và tiếp tuyến
là tọa độ tiếp điểm của đồ thị (C ) của hàm số và tiếp tuyến ![]() .
.
Ta có : ![]() , theo giả thiết
, theo giả thiết ![]() , tức là
, tức là ![]()
![]() hoặc
hoặc ![]() . Tương tự câu 1
. Tương tự câu 1
6. Gọi ![]() là tọa độ tiếp điểm của đồ thị (C ) của hàm số và tiếp tuyến
là tọa độ tiếp điểm của đồ thị (C ) của hàm số và tiếp tuyến ![]() .
.
Theo bài toán: ![]() :
: ![]()
![]() . Tương tự câu 1
. Tương tự câu 1
7. Gọi ![]() là tọa độ tiếp điểm của đồ thị (C ) của hàm số và tiếp tuyến
là tọa độ tiếp điểm của đồ thị (C ) của hàm số và tiếp tuyến ![]() .
.
Theo bài toán: ![]() :
: ![]()
![]() . Tương tự câu 1
. Tương tự câu 1
Ví dụ 2 .
1. Cho hàm số: ![]() . Tìm
. Tìm ![]() để tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng
để tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng ![]() đi qua điểm
đi qua điểm ![]() .
.
2. Gọi (Cm) là đồ thị của hàm số ![]() và (d) là tiếp tuyến của (C) tại điểm có hoành độ x = 2. Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng
và (d) là tiếp tuyến của (C) tại điểm có hoành độ x = 2. Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng ![]() .
.
Lời giải.
1. Hàm số đã cho xác định với ![]() .
.
Ta có: ![]()
Với ![]()
Phương trình tiếp tuyến tại điểm có ![]() :
: ![]()
Tiếp tuyến này đi qua ![]() nên có:
nên có: ![]()
Vậy, ![]() là giá trị cần tìm.
là giá trị cần tìm.
2. Hàm số đã cho xác định với ![]() .
.
Ta có: ![]()
Phương trình tiếp tuyến (d) : ![]()
![]()
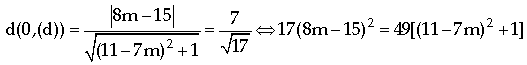
![]()
![]()