CỰC TRỊ CỦA HÀM SỐ
1. Khái niệm cực trị hàm số :
Giả sử hàm số xác định trên tập hợp ![]() và
và ![]()
![]() được gọi là một điểm cực đại của hàm số
được gọi là một điểm cực đại của hàm số ![]() nếu tồn tại một khoảng
nếu tồn tại một khoảng ![]() chứa điểm
chứa điểm ![]() sao cho:
sao cho: ![]()
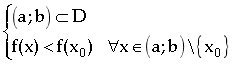 .
.
Khi đó ![]() được gọi là giá trị cực đại của hàm số
được gọi là giá trị cực đại của hàm số ![]() .
.
![]() được gọi là một điểm cực tiểu của hàm số
được gọi là một điểm cực tiểu của hàm số ![]() nếu tồn tại một khoảng
nếu tồn tại một khoảng ![]() chứa điểm
chứa điểm ![]() sao cho:
sao cho:  .
.
Khi đó ![]() được gọi là giá trị cực tiểu của hàm số
được gọi là giá trị cực tiểu của hàm số ![]() .
.
Giá trị cực đại và giá trị cực tiểu được gọi chung là cực trị
Nếu ![]() là một điểm cực trị của hàm số
là một điểm cực trị của hàm số ![]() thì ngư=ời ta nói rằng hàm số
thì ngư=ời ta nói rằng hàm số ![]() đạt cực trị tại điểm
đạt cực trị tại điểm ![]() .
.
Như vậy : Điểm cực trị phải là một điểm trong của tập hợp ![]()
Điểm cực đại , cực tiểu gọi chung là điểm cực trị của hàm số , f(x0 ) là giá trị cực trị (hay cực trị ) của hàm số.
Chú ý.
a)Giá trị cực đại (cực tiểu ) f(x0) của hàm số f chưa hẳn đã là GTLN (GTNN) của hàm số f trên tập xác định D mà f(x0) chỉ là GTLN (GTNN) của hàm số f trên khoảng (a,b) ![]() D và (a;b) chứa x0 .
D và (a;b) chứa x0 .
b)Nếu f’(x) không đổi dấu trên tập xác định D của hàm số f thì hàm số f không có cực trị .
2. Điều kiện cần để hàm số đạt cực trị:
Định lý 1: Giả sử hàm số ![]() đạt cực trị tại điểm
đạt cực trị tại điểm ![]() . Khi đó , nếu
. Khi đó , nếu ![]() có đạo hàm tại điểm
có đạo hàm tại điểm ![]() thì
thì ![]() .
.
Chú ý :
![]() Đạo hàm
Đạo hàm ![]() có thể triệt tiêu tại điểm
có thể triệt tiêu tại điểm ![]() nhưng hàm số
nhưng hàm số ![]() không đạt cực trị tại điểm
không đạt cực trị tại điểm ![]() .
.
![]() Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm
Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm
![]() Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng
Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng ![]() , hoặc tại đó hàm số không có đạo hàm .
, hoặc tại đó hàm số không có đạo hàm .
3. Điều kiện đủ để hàm số đạt cực trị:
Định lý 2: Giả sử hàm số ![]() liên tục trên khoảng
liên tục trên khoảng ![]() chứa điểm
chứa điểm ![]() và có đạo hàm trên các khoảng
và có đạo hàm trên các khoảng ![]() và
và ![]() . Khi đó :
. Khi đó :
Nếu  thì hàm số đạt cực tiểu tại điểm
thì hàm số đạt cực tiểu tại điểm ![]() .
.
Nếu 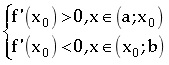 thì hàm số đạt cực đại tại điểm
thì hàm số đạt cực đại tại điểm ![]() .
.
Định lý 3: Giả sử hàm số ![]() có đạo hàm cấp một trên khoảng
có đạo hàm cấp một trên khoảng ![]() chứa điểm
chứa điểm ![]() ,
, ![]() và
và ![]() có đạo hàm cấp hai khác
có đạo hàm cấp hai khác ![]() tại điểm
tại điểm ![]() .
.
Nếu ![]() thì hàm số
thì hàm số ![]() đạt cực đại tại điểm
đạt cực đại tại điểm ![]() .
.
Nếu ![]() thì hàm số
thì hàm số ![]() đạt cực tiểu tại điểm
đạt cực tiểu tại điểm ![]() .
.
Chú ý :
1. Nếu ![]() là một điểm cực trị của hàm số
là một điểm cực trị của hàm số ![]() thì điểm
thì điểm ![]() được gọi là điểm cực trị của đồ thị hàm số
được gọi là điểm cực trị của đồ thị hàm số ![]() .
.
2. Trong trường hợp ![]() không tồn tại hoặc
không tồn tại hoặc  thì định lý 3 không dùng được.
thì định lý 3 không dùng được.
B. LUYỆN KĨ NĂNG GIẢI CÁC DẠNG BÀI TẬP.
Dạng 1: TÌM CỰC TRỊ CỦA HÀM SỐ
Bài toán 01: TÌM CỰC TRỊ HÀM SỐ TRÊN TẬP XÁC ĐỊNH.
Phương pháp giải
Tìm tập xác định D của hàm số f.
Tính f’(x).
Tìm nghiệm của phương trình f’(x) = 0 (nếu có) và tìm các điểm x0 ![]() D mà tại đó hàm f liên tục nhưng f’(x0) không tồn tại.
D mà tại đó hàm f liên tục nhưng f’(x0) không tồn tại.
Vận dụng định lý 2 (lập bảng xét dấu f’(x) ) hay định lý 3 (tính f’’(x)) để xác định điểm cực trị của hàm số.
Chú ý: Cho hàm số ![]() xác định trên D.
xác định trên D.
Điểm ![]() là điểm cực trị của hàm số khi và chỉ khi hai điều kiện sau đây cùng thảo mãn:
là điểm cực trị của hàm số khi và chỉ khi hai điều kiện sau đây cùng thảo mãn:
![]() Tại
Tại ![]() đạo hàm triệt tiêu hoặc không tồn tại
đạo hàm triệt tiêu hoặc không tồn tại
![]() Đạo hàm đổi dấu khi
Đạo hàm đổi dấu khi ![]() đi qua
đi qua ![]() .
.
Các ví dụ
Ví dụ 1 : Tìm cực trị của các hàm số sau:
1. 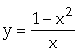 2.
2. 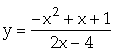
Lời giải.
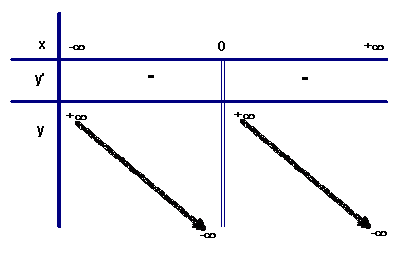
1. Tập xác định : ![]()
Ta có: 
![]() , suy ra hàm số nghịch biến trên mỗi khoảng xác định và không có điểm cực trị.
, suy ra hàm số nghịch biến trên mỗi khoảng xác định và không có điểm cực trị.
Giới hạn : ![]()
![]()
Bảng biến thiên
2. Tập xác định : ![]()
Ta có:  ,
, ![]()

Giới hạn : ![]()
![]()
Bảng biến thiên
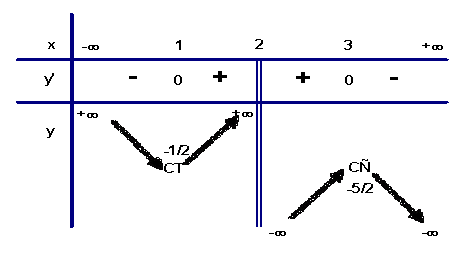
Hàm số đạt cực đại tại ![]() ,hàm số đạt cực tiểu tại
,hàm số đạt cực tiểu tại ![]() .
.
Ví dụ 2 : Tìm cực trị của các hàm số sau:
1.  2.
2. ![]()
Lời giải.
1. Tập xác định : ![]()
Ta có: ![]() ,
, ![]()
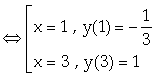 .
.
Giới hạn :  ;
;

Bảng biến thiên
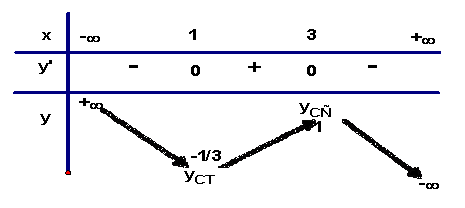
Hàm số đạt cực tiểu tại ![]() và
và ![]() ,hàm số đạt cực đại tại
,hàm số đạt cực đại tại ![]() và
và ![]() .
.
2. Tập xác định : ![]()
Ta có: ![]() ,
, ![]()

Giới hạn : ![]()
Bảng biến thiên

Hàm số đạt cực tiểu tại ![]() và
và ![]() ,hàm số đạt cực đại tại
,hàm số đạt cực đại tại ![]() và
và ![]()