PHƯƠNG TRÌNH MẶT CẦU NÂNG CAO
A – LÝ THUYẾT CHUNG
1. Định nghĩa mặt cầu
Tập hợp các điểm trong không gian cách điểm ![]() cố định một khoảng cách
cố định một khoảng cách ![]() cho trước là mặt cầu tâm
cho trước là mặt cầu tâm ![]() và bán kính
và bán kính ![]() Kí hiệu
Kí hiệu ![]()
Trong không gian với hệ trục ![]()
– Mặt cầu ![]() tâm
tâm ![]() bán kính
bán kính ![]() có phương trình là:
có phương trình là: ![]()
– Phương trình: ![]() với
với ![]() là phương trình mặt cầu tâm
là phương trình mặt cầu tâm ![]() bán kính
bán kính ![]() .
.

2. Vị trí tương đối của mặt phẳng ![]() và mặt cầu
và mặt cầu ![]()
Ø ![]() khi và chỉ khi
khi và chỉ khi ![]() không cắt mặt cầu
không cắt mặt cầu ![]()
Ø ![]() khi và chỉ khi
khi và chỉ khi ![]() tiếp xúc mặt cầu
tiếp xúc mặt cầu ![]()
Ø ![]() khi và chỉ khi
khi và chỉ khi ![]() cắt mặt cầu
cắt mặt cầu ![]() theo
theo
giao tuyến là đường tròn nằm trên mặt phẳng ![]() có tâm
có tâm
![]() và có bán kính
và có bán kính ![]()
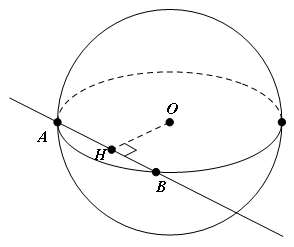
3. Vị trí tương đối giữa mặt cầu và đường thẳng
a) Cho mặt cầu ![]() và đường thẳng
và đường thẳng ![]() . Gọi
. Gọi ![]() là hình chiếu của
là hình chiếu của ![]() lên
lên ![]() và
và ![]() là khoảng cách từ
là khoảng cách từ ![]() đến
đến ![]()
 |
 |
 |
Ø Nếu ![]() thì
thì ![]() cắt mặt cầu tại 2 điểm phân biệt (H.3.1)
cắt mặt cầu tại 2 điểm phân biệt (H.3.1)
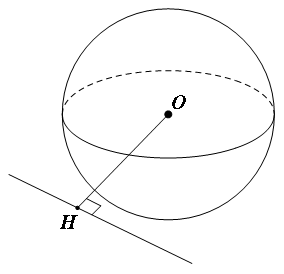
Ø Nếu ![]() thì
thì ![]() cắt mặt cầu tại 1 điểm duy nhất (H.3.2)
cắt mặt cầu tại 1 điểm duy nhất (H.3.2)
Ø Nếu ![]() thì
thì ![]() không cắt mặt cầu (H.3.3)
không cắt mặt cầu (H.3.3)
B – CÁC DẠNG TOÁN VỀ PHƯƠNG TRÌNH MẶT CẦU
Dạng 1. Biết trước tâm ![]() và bán kính
và bán kính ![]() : Phương trình
: Phương trình ![]()
Dạng 2. Tâm ![]() và đi qua điểm
và đi qua điểm ![]() :
:
· Bán kính ![]()
· Phương trình ![]() .
.
Dạng 3. Mặt cầu đường kính ![]()
· Tâm ![]() là trung điểm
là trung điểm ![]() :
: 
· Bán kính ![]()
![]()
· Phương trình ![]() .
.
Dạng 4. Mặt cầu tâm ![]() tiếp xúc mặt phẳng
tiếp xúc mặt phẳng ![]() :
:
· Bán kính 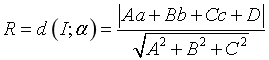
· Phương trình ![]() .
.
Dạng 5. Mặt cầu ngoại tiếp tứ diện ![]() (đi qua 4 điểm
(đi qua 4 điểm ![]() )
)
· Giả sử mặt cầu ![]() có dạng:
có dạng: ![]()
· Thế tọa độ của điểm ![]() vào phương trình (2) ta được 4 phương trình
vào phương trình (2) ta được 4 phương trình
· Giải hệ phương trình tìm ![]()
· Viết phương trình mặt cầu.
Dạng 6. Mặt cầu đi qua ![]() và tâm
và tâm ![]() :
:
· Giả sử mặt cầu ![]() có dạng:
có dạng: ![]()
· Thế tọa độ của điểm ![]() vào phương trình (2) ta được 3 phương trình
vào phương trình (2) ta được 3 phương trình
· ![]()
· Giải hệ 4 phương trình tìm ![]()
· Viết phương trình mặt cầu.
Dạng 7. Mặt cầu ![]() đi qua hai điểm
đi qua hai điểm ![]() và tâm thuộc đường thẳng
và tâm thuộc đường thẳng ![]()
Cách 1:
· Tham số hóa tọa độ tâm ![]() theo đường thẳng
theo đường thẳng ![]() (tham số
(tham số ![]() )
)
· Ta có ![]()
![]() . Giải pt tìm ra
. Giải pt tìm ra ![]() tọa độ
tọa độ ![]() , tính được
, tính được ![]() .
.
Cách 2:
· Viết phương trình mặt phẳng trung trực ![]() của đoạn thẳng
của đoạn thẳng ![]() .
.
· Tâm mặt cầu là giao của mặt phẳng trung trực trên và đường thẳng ![]() (giải hệ tìm tọa độ tâm
(giải hệ tìm tọa độ tâm ![]() )
)
· Bán kính ![]() . Suy ra phương trình mặt cầu cần tìm.
. Suy ra phương trình mặt cầu cần tìm.
(Chú ý: Nếu ![]()
![]() hoặc
hoặc ![]()
![]() thì không sử dụng được cách 2 này)
thì không sử dụng được cách 2 này)
Dạng 8. Mặt cầu ![]() có tâm
có tâm ![]() và tiếp xúc với mặt cầu
và tiếp xúc với mặt cầu ![]() cho trước:
cho trước:
· Xác định tâm ![]() và bán kính
và bán kính ![]() của mặt cầu
của mặt cầu ![]()
· Sử dụng điều kiện tiếp xúc của hai mặt cầu để tính bán kính ![]() của mặt cầu
của mặt cầu ![]()
(Xét hai trường hợp tiếp xúc trong và tiếp xúc ngoài)
Dạng 9. Mặt cầu ![]() đối xứng Mặt cầu
đối xứng Mặt cầu ![]() qua mặt phẳng
qua mặt phẳng ![]()
· Tìm điểm ![]() đối xứng với tâm
đối xứng với tâm ![]() qua mp
qua mp ![]()
· Viết phương trình mặt cầu (S’) tâm ![]() có bán kính
có bán kính ![]() .
.
Dạng 10. Mặt cầu ![]() đối xứng mặt cầu
đối xứng mặt cầu ![]() qua đường thẳng
qua đường thẳng ![]()
· Tìm điểm ![]() đối xứng với tâm
đối xứng với tâm ![]() qua mp
qua mp ![]() (xem cách làm ở phần đường thẳng)
(xem cách làm ở phần đường thẳng)
· Viết phương trình mặt cầu (S’) tâm ![]() có bán kính
có bán kính ![]() .
.
C – BÀI TẬP TRẮC NGHIỆM
Câu 1: Trong không gian với hệ trục tọa độ ![]() , cho ba điểm
, cho ba điểm ![]() và
và ![]() . Mặt cầu
. Mặt cầu ![]() tâm I đi qua
tâm I đi qua ![]() và độ dài
và độ dài ![]() (biết tâm I có hoành độ nguyên, O là gốc tọa độ). Bán kính mặt cầu
(biết tâm I có hoành độ nguyên, O là gốc tọa độ). Bán kính mặt cầu ![]() là
là
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Câu 2: Trong không gian với hệ tọa độ ![]() cho
cho ![]() Viết phương trình mặt cầu có tâm thuộc trục
Viết phương trình mặt cầu có tâm thuộc trục ![]() đi qua
đi qua ![]() và cắt mặt phẳng
và cắt mặt phẳng ![]() theo một đường tròn có bán kính nhỏ nhất.
theo một đường tròn có bán kính nhỏ nhất.
A. 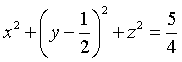 . B.
. B.  .
.
C. 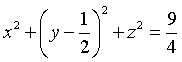 . D.
. D. 
Câu 3: Trong không gian với hệ tọa độ ![]() viết phương trình mặt cầu có tâm
viết phương trình mặt cầu có tâm ![]() và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 
A.  . B.
. B.  .
.
C.  . D.
. D. 
Câu 4: Trong không gian với hệ tọa độ ![]() cho mặt cầu có phương trình
cho mặt cầu có phương trình
![]() và đường thẳng
và đường thẳng ![]() Viết phương trình đường thẳng
Viết phương trình đường thẳng ![]() tiếp xúc mặt cầu
tiếp xúc mặt cầu ![]() tại điểm
tại điểm ![]() biết đường thẳng
biết đường thẳng ![]() tạo với đường thẳng
tạo với đường thẳng ![]() một góc
một góc ![]() thỏa mãn
thỏa mãn 
A.  . B.
. B.  .
.
C.  . D.
. D. 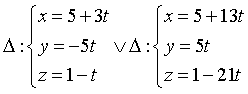
Câu 5: Trong không gian với hệ tọa độ ![]() cho đường thẳng
cho đường thẳng  Tìm tọa độ điểm
Tìm tọa độ điểm ![]() thuộc đường thẳng
thuộc đường thẳng ![]() sao cho mặt cầu
sao cho mặt cầu ![]() tâm
tâm ![]() tiếp xúc với trục
tiếp xúc với trục ![]() có bán kính bằng 2.
có bán kính bằng 2.
A.  . B.
. B. 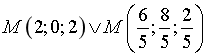 .
.
C.  . D.
. D. 
Câu 6: Trong không gian với hệ tọa độ ![]() cho hai đường thẳng
cho hai đường thẳng ![]() có phương trình:
có phương trình:  . Viết phương trình mặt cầu có bán kính nhỏ nhất và tiếp xúc với hai đường thẳng
. Viết phương trình mặt cầu có bán kính nhỏ nhất và tiếp xúc với hai đường thẳng ![]()
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]()
Câu 7: Trong không gian với hệ tọa độ ![]() cho mặt cầu
cho mặt cầu ![]()
Viết phương trình mặt phẳng ![]() chứa trục
chứa trục ![]() và cắt mặt cầu
và cắt mặt cầu ![]() theo một đường tròn có bán kính bằng 3.
theo một đường tròn có bán kính bằng 3.
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]()
Câu 8: Trong không gian với hệ tọa độ ![]() cho đường thẳng
cho đường thẳng  và cắt mặt phẳng
và cắt mặt phẳng ![]() tại điểm
tại điểm ![]() Viết phương trình mặt cầu
Viết phương trình mặt cầu ![]() có tâm
có tâm ![]() thuộc đường thẳng
thuộc đường thẳng ![]() và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng ![]() tại điểm
tại điểm ![]() biết diện tích tam giác
biết diện tích tam giác ![]() bằng
bằng ![]() và tâm
và tâm ![]() có hoành độ âm.
có hoành độ âm.
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]()
Câu 9: Trong không gian tọa độ ![]() viết phương trình mặt cầu đi qua ba điểm
viết phương trình mặt cầu đi qua ba điểm ![]()
![]() biết tâm của mặt cầu nằm trên mặt phẳng
biết tâm của mặt cầu nằm trên mặt phẳng ![]()
A.  . B.
. B.  .
.
C.  . D.
. D. 
Câu 10: Trong không gian ![]() cho 3 điểm
cho 3 điểm ![]() và mặt cầu
và mặt cầu
![]() Viết phương trình mặt phẳng
Viết phương trình mặt phẳng ![]() đi qua qua
đi qua qua ![]() song song với
song song với ![]() và tiếp xúc với mặt cầu
và tiếp xúc với mặt cầu ![]() có tâm
có tâm ![]() và có bán kính
và có bán kính ![]()
A. ![]() hoặc
hoặc ![]() .
.
B. ![]() hoặc
hoặc ![]() .
.
C. ![]() hoặc
hoặc ![]() .
.
D. ![]() hoặc
hoặc ![]()